HippopotameLe 26/06/2011 à 01:24
VI) La mesure.
En pratique, on ne voit jamais vraiment la fonction d'onde, parce que dès qu'on observe la particule, on va modifier complètement ψ.
Il faut se représenter la particule dans sa boîte comme de l'eau dans une bassine, avec des vagues à la surface. Mesurer, c'est comme plonger le doigt dans l'eau : on va effectivement se rendre compte du niveau d'eau là où on a mis le doigt, mais on va démolir tout le système de vagues.
Plus précisément, quand on interagit avec le système pour le mesurer, la fonction d'onde ψ, ce paquet de vagues compliquées, va se réduire à un seul pic très haut et très fin.
Comme ça :

C'est ça qu'on appelle la réduction du paquet d'ondes.
L'endroit où se forme le pic est aléatoire, par exemple ça pourrait plutôt être là :
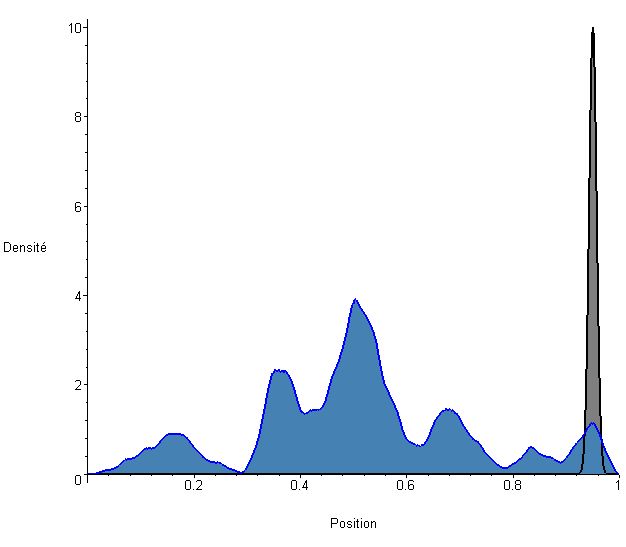
Bon en réalité ça n'est aléatoire qu'en apparence, c'est surtout chaotique et trop compliqué pour être prédit. Par contre le pic aura tendance à se former là où ψ a un module élevé.
Il est très improbable que le paquet d'ondes se réduise comme ça :

parce qu'autour de 0.29, le module de ψ est presque nul.
Du coup, quand on mesurera la position de la particule, on la verra bien ponctuelle, en un seul x.
x=0.55 dans le premier exemple, x=0.95 dans le second, x=0.29 dans le troisième.
Et la probabilité de voir la particule en un certain point est donc bien proportionnelle à la valeur de |ψ|² à cet endroit.
Une fois qu'on a fini de mesurer, donc d'interagir, ben la fonction d'onde va petit à petit se réétaler...
Donc ouais on casse l'état de départ, mais on n'aboutit pas du tout à un état d'énergie pur, au contraire on aboutit à une superposition d'énergies très élevées (c'est logique, si on touche la particule, on va l'exciter...).
Par contre on aboutit à un état de position pur.
Réciproquement, si on mesurait l'énergie, le système se projetterait aléatoirement sur un état d'énergie pur (avec une probabilité proportionnelle à la norme du coefficient de Fourier correspondant...), l'un de ceux que j'ai représentés plus haut. Par contre ça ne serait pas du tout un état de position pur (puisque ça serait une sinusoïde étalée dans toute la boîte).
Tout ça illustre que dans l'espace des états possibles de la particule ( L²([0,1]), qui est un espace de Hilbert), il y a deux bases orthogonales naturelles : celle des états d'énergie purs (c'est à dire les vecteurs propres de l'opérateur "énergie", qui sont les sinusoïdes) et celle des positions pures (les vecteurs propres de l'opérateur "position", qui sont les Dirac).
L'impossibilité de tomber à la fois sur un état pur d'énergie et de position est équivalent au fait que ces deux bases ne coïncident pas, et qu'elles sont même assez éloignées, d'une manière précisée par le principe d'incertitude de Heisenberg (qui est en réalité un théorème mathématique).
En pratique, on ne voit jamais vraiment la fonction d'onde, parce que dès qu'on observe la particule, on va modifier complètement ψ.
Il faut se représenter la particule dans sa boîte comme de l'eau dans une bassine, avec des vagues à la surface. Mesurer, c'est comme plonger le doigt dans l'eau : on va effectivement se rendre compte du niveau d'eau là où on a mis le doigt, mais on va démolir tout le système de vagues.
Plus précisément, quand on interagit avec le système pour le mesurer, la fonction d'onde ψ, ce paquet de vagues compliquées, va se réduire à un seul pic très haut et très fin.
Comme ça :
C'est ça qu'on appelle la réduction du paquet d'ondes.
L'endroit où se forme le pic est aléatoire, par exemple ça pourrait plutôt être là :
Bon en réalité ça n'est aléatoire qu'en apparence, c'est surtout chaotique et trop compliqué pour être prédit. Par contre le pic aura tendance à se former là où ψ a un module élevé.
Il est très improbable que le paquet d'ondes se réduise comme ça :
parce qu'autour de 0.29, le module de ψ est presque nul.
Du coup, quand on mesurera la position de la particule, on la verra bien ponctuelle, en un seul x.
x=0.55 dans le premier exemple, x=0.95 dans le second, x=0.29 dans le troisième.
Et la probabilité de voir la particule en un certain point est donc bien proportionnelle à la valeur de |ψ|² à cet endroit.
Une fois qu'on a fini de mesurer, donc d'interagir, ben la fonction d'onde va petit à petit se réétaler...
Sally (./69) :
ce qui est bizarre c'est que j'avais cru comprendre qu'en interagissant trop avec la particule on cassait la superposition d'états et la particule se retrouvait dans un état pur, mais là la forcer à se concentrer spatialement revient à faire exactement le contraire...
Donc ouais on casse l'état de départ, mais on n'aboutit pas du tout à un état d'énergie pur, au contraire on aboutit à une superposition d'énergies très élevées (c'est logique, si on touche la particule, on va l'exciter...).
Par contre on aboutit à un état de position pur.
Réciproquement, si on mesurait l'énergie, le système se projetterait aléatoirement sur un état d'énergie pur (avec une probabilité proportionnelle à la norme du coefficient de Fourier correspondant...), l'un de ceux que j'ai représentés plus haut. Par contre ça ne serait pas du tout un état de position pur (puisque ça serait une sinusoïde étalée dans toute la boîte).
Tout ça illustre que dans l'espace des états possibles de la particule ( L²([0,1]), qui est un espace de Hilbert), il y a deux bases orthogonales naturelles : celle des états d'énergie purs (c'est à dire les vecteurs propres de l'opérateur "énergie", qui sont les sinusoïdes) et celle des positions pures (les vecteurs propres de l'opérateur "position", qui sont les Dirac).
L'impossibilité de tomber à la fois sur un état pur d'énergie et de position est équivalent au fait que ces deux bases ne coïncident pas, et qu'elles sont même assez éloignées, d'une manière précisée par le principe d'incertitude de Heisenberg (qui est en réalité un théorème mathématique).