VII Espace des phases, bases orthogonale et observables



Maintenant, un petit peu plus sur les quantités observables : je vais développer la fin de ./73.
Il y aura un peu de maths (algèbre linéaire).


Or donc on a vu que l'espace des phases ( = ensemble des états du système = ensemble des fonctions d'onde possibles) est l'espace L²([0,1]).

C'est à dire l'ensemble des fonctions ψ : [0,1] -> C, qui vérifient ψ(0)=ψ(1)=0, qui sont continues et telles que |ψ|² est intégrable..

Remarquons que c'est un espace de Hilbert.
C'est à dire que c'est un espace muni d'un produit scalaire (complexe... ce qu'on appelle un produit hermitien), pour lequel L²([0,1]) est un espace complet (mais peu importe ce genre de détail).

Le produit scalaire de phi et ψ est noté <phi|ψ> (c'est la notation bra-ket de Dirac) et est donné par la formule (chère à tous les taupins de France) :




Le cas de l'énergie

On a vu qu'il y a des états d'énergie purs, indexés par les entiers k non nuls, donnés par .

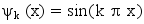On peut vérifier que 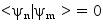pour n et m deux entiers distincts, c'est un exercice de calcul intégral très classique. Ça signifie que les états ψk sont orthogonaux.

De plus, toute fonction ψ de L²([0,1]) s'écrit => c'est la décomposition de Fourier.


En résumé :

Les états d'énergie purs ψk forment une base orthogonale de L²([0,1]).
À chaque vecteur de cette base correspond une énergie - ici k²E1.




Le cas de la position

Les états de position purs sont les Dirac , pour chaque point x de ]0,1[.

Il est clair que deux Dirac et ont un produit scalaire nul si x et y sont différents. De plus toute fonction d'onde psi s'écrit comme somme de Diracs coefficientés (voir quand même plus bas).

Les positions pures forment donc une base orthogonale de L²([0,1]), et à chaque position pure correspond une mesure x de la position de la particule.




Le cas général

Bien entendu tout cela se généralise.

À chaque fois qu'on a une quantité observable, il y a une base orthogonale de L²([0,1]) correspondante, et à chaque vecteur de cette base est associé une mesure possible de cet observable.


Au moment où on fait la mesure, la fonction d'onde est projetée sur l'un des états purs , de façon non prédictible mais une probabilité proportionnelle à . La quantité mesurée est le correspondant au sur lequel on est tombé.




Tout cela admet une formulation mathématique plus simple et élégante.

On va dire qu'un observable est un opérateur hermitien de L²([0,1]).

C'est à dire une application linéaire A : L²([0,1]) -> L²([0,1]) qui vérifie .


Par exemple, l'observable R de position est l'opérateur R défini par .

Il y a un théorème qui dit que tout opérateur hermitien est diagonalisable dans une base orthogonale. => Les vecteurs propres de l'opérateur forme la base orthogonale évoquée plus haut, les valeurs propres sont les résultats de la mesure.

On peut effectivement vérifier que les vecteurs propres de sont les Dirac .



Quelques opérateurs classiques :

Position :

Impulsion :

Énergie (aussi appelé hamiltonien) :
(On reconnait dans le premier terme le carré de l'opérateur impulsion, divisé par 2m... donc l'énergie cinétique. Le second terme est l'énergie potentielle).

Moment angulaire :
(le produit vectoriel des opérateurs position et impulsion... logique)



Précisions mathématiques

Il y a de gros pipeaux dans ce que j'ai dit à propos de la position.

1) Les diracs ne sont pas des éléments de L²([0,1]). Il faudrait parler de distributions.

2) Quand bien même : on ne peut pas multiplier deux distributions, dont on ne peut pas calculer le produit scalaire de deux diracs.

3) Et de toute façon c'est un peu louche de dire qu'une fonction est une somme de diracs coefficientés.


Bref tout cela était juste "avec les mains", mais en toute rigueur faux.
Mais qu'à cela ne tienne : la notion d'opérateur est justement utile pour éviter ces petites emmerdes mathématiques, l'opérateur position est défini de façon tout à fait rigoureuse et satisfaisante.




Exercice : pour chaque opérateur, on peut calculer les états propres, dans le cas d'une particule dans une boîte, et voir si les valeurs propres sont quantifiées ou continues...
Le papier de Schrödinger en 1926, "Quantisierung als Eigenwertproblem" ("la quantification comme problème de valeurs propres") est considéré comme l'un des plus importants du XXième siècle.