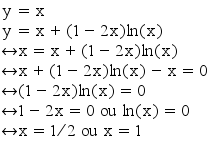Logarithme népérien - Page 1

Salut à tous!
J'aurai une petite question, voilà je n'arrive enfin je ne sais plutôt pas comme fait pour calculer la limite quand x tend vers 0 et +infini de f(x)=x+(1-2x)ln(x).

Pouvez vous m'aider ou m'expliquer comment faire svp ?
Merci car ca me bloque pour continuer mon DM!

Bonnes fêtes

Gaëlle

Quand x tend vers 0, c'est simple, la limite est -

Quand x tend vers +, on a .

La limite en + de ln(x)/x étant une propriété du cours, normalement tu devrais avoir ta limite en multipliant par les bons bouts ^^

Et la limite en zéro je peux l'écrire directement ou il faut que je détaille ?

Je suis entrain de calculer l'autre!

Merci!

Pour celle en +infini, je n'avais pas vu sur mon énoncé il est dit que

Donc j'ai fait :
Lim quand x tend vers +infini de x = +infini
Lim quand x tend vers +infini de = ?? ca je n'arrive pas à trouver , je ne suis pas sure de moi, ca fait 0 ?!

quelle est la limite de chacun des éléments de la somme ?

Oui oui loool j'allais venir éditer mon message, je viens de tout refaire calmement :

Limite quand x tend vers 0 de x+(1-2x)ln(x)
Lim(x)=0
Lim(1-2x)=1
Lim(ln(x))=-infini
Donc limf(x)=-infini (limite d'une somme)



Limite quand x tend vers +infini de
Lim(x)=+infini
Lim () :
-Lim(1)=1
-Lim(ln(x)/x)=0
-Lim(ln(x))=+infini
Donc Lim ()=-inf (limite d'une somme)
Donc Limf(x)=-inf (limite d'un produit)

Mais bon c ne m'avance pas a grand chose!
Cer je bloque pour la question suivante!

Il faut que je calcule la dérivée de F
Est-il plus facile d'utiliser la fonction d'origine soit f(x)=x+(1-2x)ln(x) ou f(x)= ?

à ton avis ? c'est plus simple de calculer les dérivées quand il y a un quotient ou quand il n'y en a pas ?
de toute façon peu importe la formule que tu choisis, tu devrais arriver au même résultat . Éventuellement tu peux faire les deux pour vérifier que tu ne te trompes pas ^^. Tu sais comment on calcule la dérivée d'un produit, non ? et d'une somme, aussi ? et tu connais la dérivée de ln x ? si oui, alors je ne vois vraiment pas la difficulté...

Au final ca me fait -2ln(x)+(1-x/x) voilà! ce que je devais trouver!
Et puis Sally ce n'est pas que c'était difficile, c'est juste que je ne savais pas par où commencer!

d'accord
ta formule est juste, mais il me semble que 1 – x/x devrait se simplifier, non ? ^^

Bah je vois pas comment les x ne peuvent pas s'éliminer... si ??
Enfin c'est ce que je devais trouver, fallait que je prouve que f'(x) donner ce résultat!

Par contre j'ai une question après faut que j'étudie le signe de -2ln(x) , celui de 1-x/x et de f'(x) , mais comment on fait sachant que c'est une addition ? Je ne vois pas comment factoriser, donc je ne vois pas comment faire... :s Parce que même en étudiant le signe de chacun on ne peut pas trouver au final celui de f'(x) si ?

Sur ce , Bonne et heureuse année 2006 à tous!

tu es sûre que dans x/x tu ne peux pas éliminer x (je te rappelle que x ne peut pas être égal à zéro, ce n'est pas dans le domaine de définition de ta fonction ^^)

Oui je suis d'accord, mais je devais montrer que c'est égal à cela, et après faut bien que j'étudie le signe de 1-x/x , c'est bien marqué dans mon énoncé... Donc , je sais pas s'il faut que je les élimine ou non :s

(1-x)/x = 1/x - 1

positif si x < 1 et x différent de 0, négatif si x > 1.

Toujours faire des petits calculs pour voir si on peut pas simplifier des fonctions...

Ok Sally & Yoshi Noir!

Par contre j'ai une question après faut que j'étudie le signe de -2ln(x) , celui de 1-x/x et de f'(x) , mais comment on fait sachant que ce n'est pas un facteur ou une division ? Je ne vois pas comment factoriser, donc je ne vois pas comment faire... :s Parce que même en étudiant le signe de chacun on ne peut pas trouver au final celui de f'(x) si ?

ah pardon c'est (1–x)/x (parce que sinon chez moi 1–x/x ça vaut 0)
donc j'avais mal compris et on ne pouvait pas vraiment simplifier

euh donc, retrouver le signe d'une somme à partir des signes des termes n'est pas toujours possible, tu as raison. En fait, *si* les deux termes sont de signes différents, ce n'est pas possible. Mais par contre, s'ils sont de même signe, tu sais qu'obligatoirement la somme aura le même signe que les deux termes

Donc comme ça :

Soient x=0 et x=1 les valeurs interdites.
-2ln(x) est de signe positif sur ]0;1[
-2ln(x) est de signe négatif sur ]1;+inf[

(1-x)/x est de signe positif sur ]0;1[
(1-x)/x est de signe négatif sur ]1;+inf[

Donc f'(x) est de signe positif sur ]0;1[ et de signe négatif sur ]1;+inf[.

En plus ca colle bien pour refaire mon tableau de variation de f, qui correspond bien à celui trouvé graphiquement!

Merci beaucoup!

Ensuite il faut que je résoude (1-2x)ln(x)=0
Donc j'ai mis :

Il faut que x soit strictement supérieur à 0
L'ensemble de définition de l'équation est ]0;+inf[

Par contre après j'ai un soucis, on a vu en cours que pour résoudre cela faut mettre des ln des deux côtés.

Donc le 0 = ln(1)
On a le ln(x)
Mais je ne trouve pas comment mettre des ln avec (1-2x) , car j'ai pas le droit de mettre ln(1)-ln(2x) et après transformer..
J'ai regardé les exemples de mon cours, dans mon livre et je n'ai jamais ce cas de figure..

Galloute (./19) :
que je résoude

Biiiip.

---

(1-2x)*ln(x)=0

Le produit est nul si au moins l'un des deux facteurs est nul. Donc :

Solutions :

1-2x=0
2x=1
x=1/2

ou x=1.

Résolve désolé mdr
Ah je voulais me compliquer la vie moi! :s
Merci!

Yoshi Noir (./20) :

Galloute (./19) :
que je résoude

Biiiip.

---

(1-2x)*ln(x)=0

Le produit est nul si au moins l'un des deux facteurs est nul. Donc :

Solutions :

1-2x=0
2x=1
x=1/2

ou x=1.

Mais le ln il s'enlève tout seul alors ?

EDIT : AH NON J'AI COMPRIS LN(1)=0 lool
désolé je suis longue à comprendre!

Après faut que j'en déduise les coordonnées des points d'intersection de la courbe C et de la droite DELTA d'équation y=x... C'est à partir des solutions de l'équation que je peux les trouver ?

eh bien ta courbe a pour équation y = f(x), ses points d'intersection avec la droite Delta sont les points qui sont à la fois sur la courbe et la droite, c'est-à-dire les points qui vérifient à la fois l'équation de la courbe et celle de la droite, c'est-à-dire les points (x,y) tels que : y = x ET y = f(x).

Donc déjà, il faut trouver les valeurs possibles de x, n'est-ce pas ? tu dois pouvoir facilement écrire une équation où y n'intervient pas à partir des deux précédentes, et elle devrait ressembler à celle que tu viens de résoudre

(1-2x)ln(x)=x ??
Ca doit pas être ça, je ne vois pas trop ce que ça peut etre ...
J'ai du mal à comprendre surtout qu'on ne l'a fait en cours, alors grr...

Ben si c'est ça...

mais non, c'est pas ça...
tu as y = x et y = f(x), vous n'avez pas fait les systèmes d'équations ?
en fait tu peux dire que la première équation te donne la valeur de y en fonction de x (y = x) et ensuite dans la deuxième tu fais une substitution, tu remplaces y par sa valeur c'est-à-dire par x, donc tu obtiens x = f(x). Voilà l'équation qu'il te faut résoudre .

Ensuite quand tu auras trouvé les valeurs de x possibles, il te suffira de reprendre la première équation (y = x) pour retrouver les valeurs de y correspondantes

edit : cross
yoshi noir > non, c'est pas f(x) ce qu'elle a écrit (cf. ./1)

Ah OK
À force de la voir poser des questions, j'en avais oublié la fonction principale

Je vais essayer Sally, mais en fait ce qui est bizarre c'est que l'on a rien fait de ce genre dans ce chapitre, c'est pour cela que j'ai du mal à comprendre!

Désolé Yoshi Noir, j'essaie de comprendre mon DM et d'y arriver dans mes études!

Je ne suis pas sure que ce soit bon...

Si, c'est bon, mais fais attention aux doubles flèches, tu as bien des équivalences la plupart du temps mais pas quand tu passes du système d'équations à l'équation sans les y (pour avoir une vraie équivalence, il faudrait écrire : x = x + (1–2x)ln x ET y = x). Donc évite d'utiliser une double flèche à cet endroit-là, on peut te retirer des points pour cela. Bon je ne sais pas si tu rédigerais ton devoir comme tu l'as écrit ici, mais globalement n'hésite pas à mettre des phrases en français qui expliquent ce que tu fais et pourquoi ça marche, cela prouvera que tu as bien compris...
pas forcément à chaque étape (genre quand tu retranches x des deux côtés de l'équation, c'est pas la peine d'écrire un roman à ce sujet), mais pour les étapes où il y a un peu de raisonnement : donc celle où tu substitues x à y dans la seconde équation, et aussi éventuellement (ça ça va dépendre des profs, mais ça ne peut pas faire de mal) quand tu dis qu'un produit est nul si et seulement si l'un des facteurs est nul.
Ah sauf que la fin c'est en fait ce que tu as fait dans la question précédente, c'est ça ? ben dans ce cas, plutôt que de recopier les étapes que tu avais déjà faites, écris en français : on reconnaît l'équation de la question machin, dont les solutions sont 1/2 et 1. Ce sera plus clair pour tout le monde

D'ailleurs ce n'est pas que pour le prof, c'est aussi pour toi : si à un moment tu n'arrives plus à expliquer comment tu passes d'une étape à la suivante, cela pourra vouloir dire que tu t'es peut-être trompée, ou qu'il manque des étapes intermédiaires...