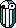Equation de la courbe: p(o)=sin(o)/o
L'ensemble de définition je dirai R*
Pour la réduction de l'ensemble de définition a priori il me semble qu'on ne peut qu'utiliser la parité. M(-o)=M(o) (symétrique par rapport à Ox)
Le signe et les variations de p:
p'(o)=(ocos(o)-sin(o))/o² (si je ne me suis pas trompé)
Le signe de cette dérivée n'étant pas tout à fait trivial je suppose qu'il faut étudier la fonction ocos(o)-sin(o)=g(o) (sur [0,2pi] ?)
La dérivé donne -osino on en déduit le signe de g' et les variation de g. A partir des variation de g on arrive à déduire le signe de g sur certain interval. On sait également qu'elle est croissante strictement et continue sur pi,2pi et que g(pi)=-pi et g(2pi)=2pi donc sur [pi,2pi] l'équation g(o)=0 admet une unique solution on a donc ocoso-sino=0 si cos o<>0 alors o=tan( o) ? si cos o=0 alors o=pi/2[pi]?
Enfin bref je me suis magistralement embrouillé et n'arrive pas à trouver mes erreurs je n'obtient pas le signe de la dérivé.
Et puis p(o) semble s'annuler une infinité de fois comment étudier ces points ?
Je n'arrive pas à installer maple (l'installation ne veut pas se lancer
) sur mon ordi je ne sais même pas à quoi ressemble cette courbe.
)
