Je suis en Master1 d'informatique et j'ai écopé d'un sujet qui, à mon grand damn, me frappe sur une faiblesse d'assez longue date : les mathématiques ...
Je m'explique : Je dois réaliser un programme qui factorise (si possible) dans Z/pZ un polynôme (univarié ou multivarié) de degré n.
Les recherches que j'ai effectué m'ont permis d'aboutir à deux méthodes :
Cantor - Zassenhaus, qui utilise des corps, des anneaux et d'autres trucs auxquels je ne comprends rien :/
Berlekamp, qui utilise de l'algèbre linéaire, certes un peu plus facile à cerner, mais dont l'application pour cet exercice me plonge dans le désespoir le plus total.
Je poste ce topic, non pas pour y trouver une super méthode magique, mais dans l'espoir que l'un d'entre vous connaisse un lien, une réference, un article quelconque, n'importe quoi, qui pourrait faire usage d'un minimum de vulgarisation dans l'explication de tels concepts.
Merci de m'avoir lu

PS : ce projet m'a fait apprendre un nouveau mot hier : Abscons




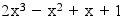

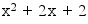









 alleluia
alleluia 


