Plus les énigmes progressent, plus le nombre de signaux disponibles (connu) et le nombre de signaux à superposer (inconnu) augmente. On peut aussi bien avoir 6 signaux dispos et 4 à additionner, que 12 dispos et 3 à additionner.
Exemple de la dernière énigme :
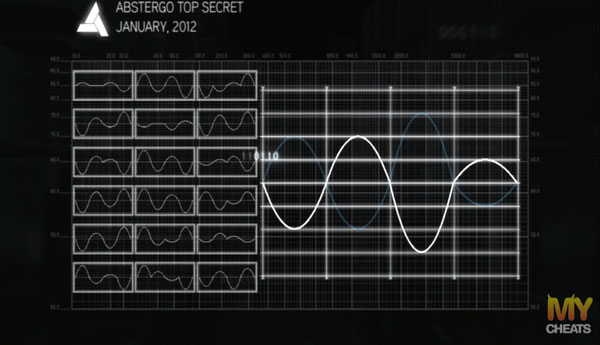
(en blanc le signal à obtenir, en bleu le résultat du cumul actuel)
Dans les premiers, le résultat était assez simple, il suffit de regarder deux minutes pour trouver la combinaison.
Par la suite, je me suis mis à les réduire à l'état de nombre (chaque signal étant quatre courbes d'amplitude 4 à -4) en cherchant quelles combinaisons pouvaient former la première courbe, puis sur les signaux restants quelles combinaisons pouvaient former la seconde, etc.
Vers la fin, en gagnant en complexité, je me suis mis à écrire un script qui allait résoudre pour une combinaison de jusqu'à 4 signaux, avec une imbrication de quatre boucles.
Sur le dernier, j'ai refait le script en utilisant une récursive pour résoudre n'importe quel combinaison max donnée (pour 18 signaux par exemple, je sais qu'il ne peut y avoir que de 2 à 18 signaux cumulés).
Je propose aux intéressés de donner leur version, dans le langage de leur choix (langage "lisible" si possible
 ) de leur façon de résoudre cette énigme.
) de leur façon de résoudre cette énigme.Pour résumer : on peut voir un signal comme des tableaux de 4 entiers compris entre 4 et -4, et le cumul des signaux est une simple addition de ces tableaux ([0, 1, 2, 3] + [4, -3, 0, 0] = [4, -2, 2, 3]).
Pour un signal solution donné, et une série de signaux donnés (les deux étant écrits en dur dans le code, faisons au plus simple), proposez un code qui permet de trouver une (ou toutes, mais l'important reste de résoudre l'énigme) solution, sachant que ce code doit être réutilisable d'une énigme à l'autre en changeant uniquement le contenu des variables de la solution et des signaux à utiliser.
L'ayant fait à domicile, je proposerai ma version une fois rentré chez moi.


