
Pavé

Quelques gif de quelques Mo
Les discussions de tantôt sur la mécanique quantique m'ont donné envie de voir un peu plus précisément de quoi il s'agit et comment marchent les équations ; du coup j'ai rédigé un petit bazar pour voir si j'avais compris.
Mon but était de réussir à calculer d'un bout à l'autre l'évolution d'un système quantique très simple.
Or donc on va considérer un objet quantique.
On suppose que c'est un objet sans qualité, c'est à dire qu'à part la position et la masse, il n'a rien de particulier (pas de charge électrique ou truc du genre).
On va supposer que cet objet est enfermé dans une boîte. Et pour simplifier, on va supposer qu'on est dans un univers à 1 dimension (ça marche essentiellement pareil en 3 dimensions, seulement les dessins et les calculs sont carrément plus durs à faire).
Donc la boîte, ça va être le segment [0,1].
I) Qu'est ce que c'est qu'un objet quantique ?
En mécanique classique, l'objet aurait une certaine position 0 < x < 1, et puis voilà.
Exemple : x=0.65
En mécanique quantique, l'objet n'a pas de position bien définie, il a partout dans la boîte une certaine
présence. Cette présence est mesurée, en chaque point de la boîte, par un certain nombre complexe Z=X+iY.
Plus le module de ce nombre complexe est grand, plus la particule est "présente" en ce point ; plus |Z| est petit, plus elle est absente.
Plus précisément, la densité de présence est proportionnelle à |Z|² = X²+Y², le carré du module.
Ce Z qui dépend de la position x s'appelle la fonction d'onde, elle est notée ψ(x).
Voilà un exemple :
J'ai fabriqué (un peu au pif) l'état d'une particule, que j'ai représenté par des graphiques de fonctions.
D'abord, la partie réelle X (en vert) et imaginaire Y (en rouge), en fonction de la position :
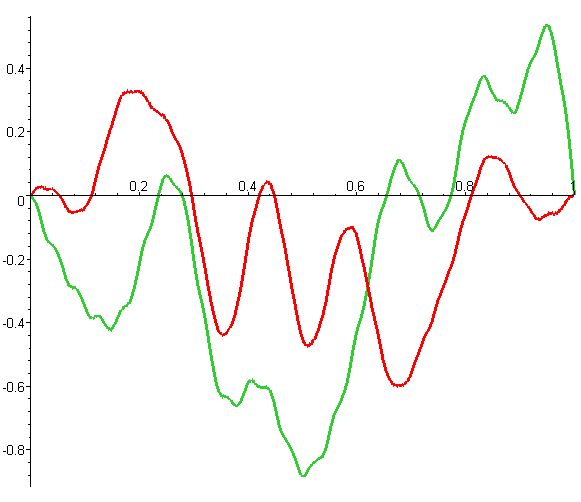
À partir de là, on peut calculer la densité de présence |ψ(x)|² = X²+Y² :

(La fonction est normalisée pour que l'aire en bleu vaille 1).
Quand on fait une mesure, la probabilité de trouver la particule à un endroit est proportionnelle est la hauteur de la courbe à cet endroit. Par exemple, la probabilité de voir la particule entre 0.4 et 0.6 est proportionnelle à l'aire suivante :

En faisant le calcul, on trouve 0.458918..... (c'est l'intégrale de |ψ|² entre 0.4 et 0.6)
Autrement dit, on a à peu près 46% de chance de voir la particule entre 0.4 et 0.6. On voit qu'on n'a quasiment aucune chance de la voir près de 0.3, pas mal de chance près de 0.7, etc...
Donc récapitulons :
Une particule, c'est une fonction d'onde ψ(x).
ψ est une fonction qui va de [0,1] (la boîte) ou R (l'espace) dans l'ensemble des nombres complexes.
Elle est continue (et donc, pour une boîte, on a forcément ψ(0)=0 et ψ(1)=0).
L'intégrale de |ψ|² vaut 1.
II) Comment ça évolue ?
La densité de présence que j'ai donnée n'est valable qu'à un instant t.
Comme n'importe quel autre objet physique, tout ça va évoluer au fil du temps, selon des lois qu'on a su expliciter.
Tout calcul fait, la densité de présence |ψ|² tracée plus haut va évoluer de la façon suivante (j'expliquerai après comment on a fait le calcul) :

La fonction d'onde elle même, ψ, évolue comme ça (la partie réelle est toujours en vert et la partie imaginaire en rouge) :
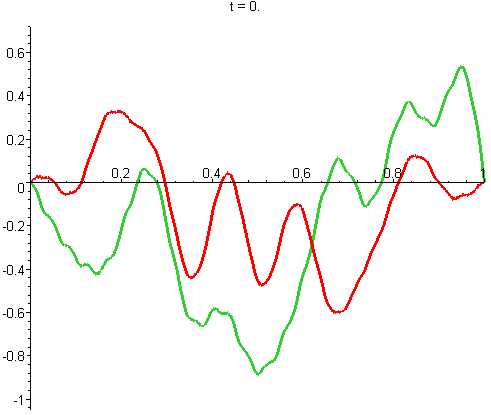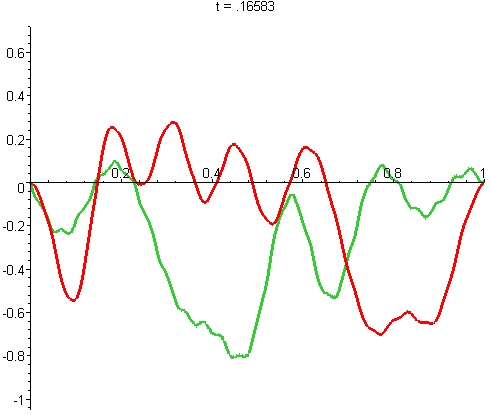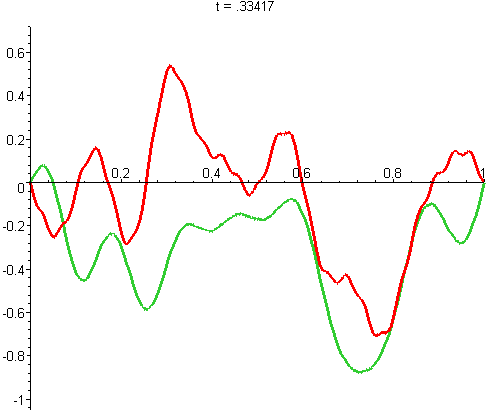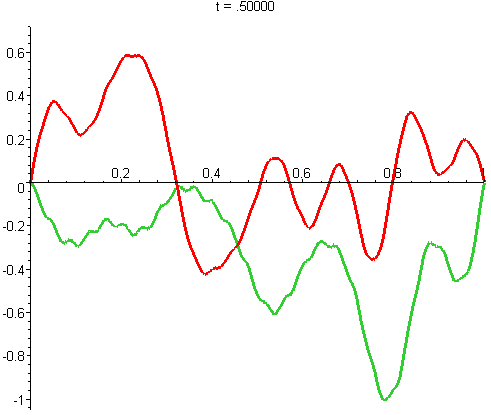
J'ai aussi fait un gif avec une échelle temporelle 5 fois plus fine, pour bien voir les détails de l'évolution (le petites vagounettes bougent vite, les grandes vagues bougent doucement) :
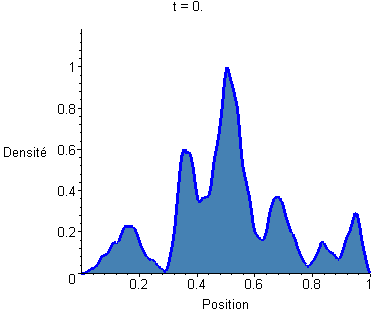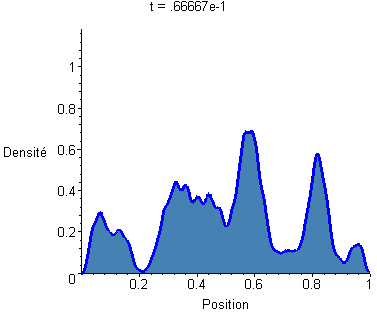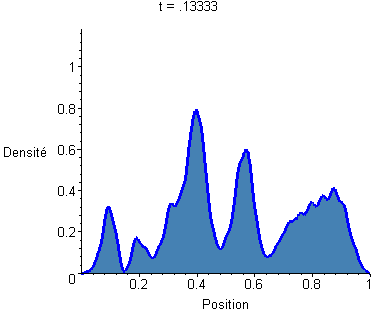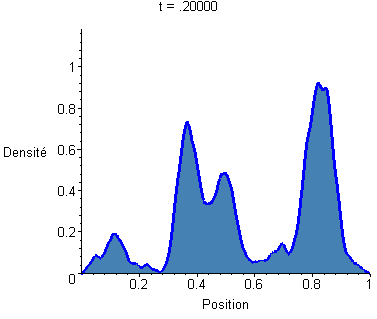 III) L'énergie
III) L'énergie
C'est l'
équation de Schrödinger qui gouverne l'évolution de la fonction d'onde, c'est à dire qui permet de calculer ψ(x,t) en fonction de la condition initiale ψ(x,0).
La forme de cette équation est assez simple, c'est
grosso modo "Énergie = constante", et donc "La dérivée de l'énergie est nulle".
Reste à savoir ce qu'est l'énergie de notre particule ! Schrödinger est parti de la même expression de l'énergie qu'en mécanique classique :
Énergie mécanique = Énergie cinétique + Énergie potentielle
- Dans mon exemple je suppose qu'il n'y a pas d'énergie potentielle, donc on va juste remplacer ça par 0.
Mais s'il y avait dans l'espace un champ gravitationnel, un champ électrique ou quelque chose comme ça, il faudrait en tenir compte.
Dans ce cas on aurait un potentiel V(x) dépendant de la position, et pour avoir le potentiel de la particule, il suffirait d'additionner pour chaque point x de l'espace le produit du potentiel V(x) et de la densité de présence de la particule, autrement dit calculer l'intégrale de V(x)ψ(x).
- Pour l'énergie cinétique, c'est plus délicat. En principe, elle vaut 1/2 mv² où v est la vitesse de la particule (ou encore p² / 2m où p est l'impulsion, en mécanique quantique on préfère cette forme).
Le problème c'est que la vitesse est la dérivée de la position, or on n'a pas de position précise à dériver !
La solution est la suivante. On va commencer par décomposer la fonction ψ(x) en série de Fourier (c'est à dire en une somme de sinusoïdes, avec des coefficients complexes)
Dans l'exemple,

= (-0.79 -0.42i)*
+ (-0.45 +0.33i)*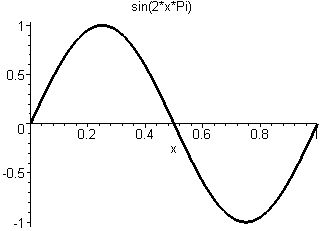
+ (0.56 +0.26i)* 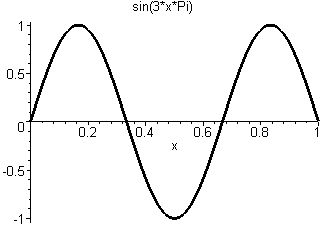
+ (-0.23 -0.04i)* 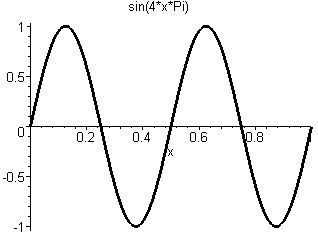
+ ... (moultes autres composantes)
Comme l'équation de Schrödinger est linéaire, il suffit de calculer l'évolution de chaque composante, puis de refaire la combinaison linéaire des solutions.
Chaque composante étant une sinusoïde avec une longueur d'onde bien définie, on peut appliquer la relation de de Broglie :
λ = h / p
où
λ est la longueur d'onde,
h = 6,626*10^-34 J.s est la constante de Planck,
p est l'impulsion.
C'est une généralisation d'une égalité déjà vérifiée dans le cas de la lumière (du photon). Le brave de Broglie a eu le prix Nobel pour cette idée.
Alors par exemple, la composante

a une longueur d'onde λ = 2/3 (crête à crête), donc une impulsion p = h/λ = 3h/2 et une énergie E = p²/2m = 9h²/8m.
(attention aux unités, mon λ était une longueur)
De façon générale, la composante sin(k Pi x) aura une énergie égale à k²E1, où E1=h²/8m.
Maintenant, quelques remarques :
- Ma particule de départ n'a pas d'énergie bien définie. Il ne faut surtout pas croire qu'elle aurait une "énergie moyenne" qui serait la somme coefficientée des énergies de ses différentes composantes. Ça ne marche pas comme ça. Il faut dire plutôt qu'elle est une superposition (ou combinaison linéaire) d'états d'énergies différentes.
- On voit que l'énergie d'une particule enfermée dans une boîte est quantifiée. Elle peut valoir E1, 4 E1, 9 E1, 16 E1, 25 E1... mais pas 3 E1 ou 0,5 E1.
- La particule est dans l'état d'énergie minimal (ou état fondamental, ou état non excité), quand sa fonction d'onde ψ(x) a pour module sin(Pi x). Sa densité de présence ressemble alors à

Contrairement à ce qui se passe en mécanique classique, l'énergie de l'objet n'est pas nulle même dans cet état d'énergie minimale.
- Quand la particule est dans un état d'énergie pure, la fonction d'onde garde un module | sin(k Pi x) | constant au fil du temps : la densité de présence ne varie pas. Par contre, la phase varie.
Dans un état d'énergie pure, la fonction d'onde est donc du type ψ(x,t) = sin(k Pi x) e^(i f(t))
IV) Évolution des états d'énergie purs.
L'équation de Schrödinger (sous l'une de ses formes) s'écrit
iħ dψ/dt = -ħ²/2m d²ψ/dx² + V ψ
où
V(x) est le potentiel, donc ici 0,
ħ = h/2Pi est la constante de Planck réduite.
Il suffit de remplacer ψ par sin(k Pi x) e^(i f(t)), malgré l'allure barbare de l'équation, le calcul est facile et on va trouver que f'(t) = -i E1 k² / h
On aura donc
ψ(x,t) = sin(k Pi x) e^(i Constante k²) pour l'état d'énergie k²E1.
Voilà par exemple l'état k=1 (en vert et rouge les parties réelles et imaginaires de ψ, en bleu la densité de présence) :
Et l'état k=3 (en vert et rouge les parties réelles et imaginaires de ψ, en bleu la densité de présence) :
La vitesse d'évolution de la phase dépend du carré de k.
Quant à ma particule de départ, j'ai décomposé la fonction d'onde initiale en combinaison linéaire d'états purs, j'ai calculé l'évolution de chacun de ces états, j'ai recombiné tout ça et j'ai donc trouvé ce que j'avais mis plus haut :
 V) Un peu plus loin.
Et si la particule n'était pas enfermée dans une boîte ?
V) Un peu plus loin.
Et si la particule n'était pas enfermée dans une boîte ?
La différence, c'est que l'énergie ne serait pas quantifiée. Tous les sin(truc*x) sont autorisés.
Et en trois dimensions ?
Voici par exemple les états d'énergie purs pour une particule enfermée dans un cube, ou dans une pyramide :
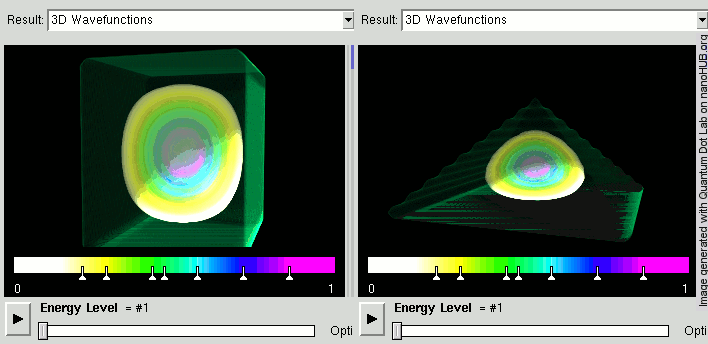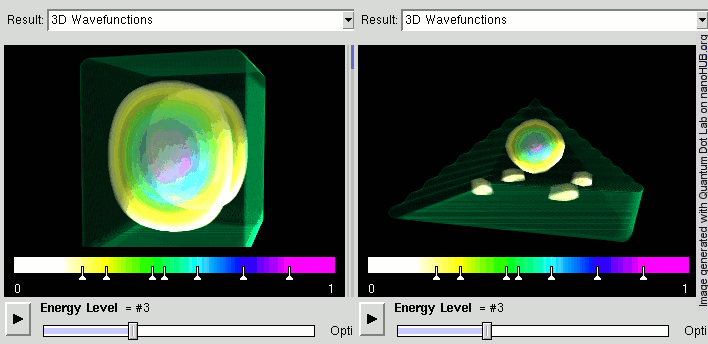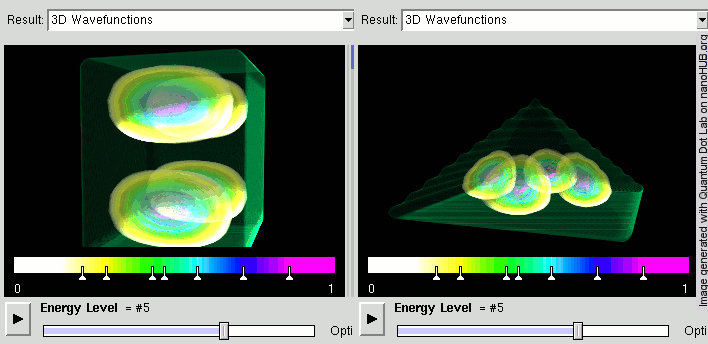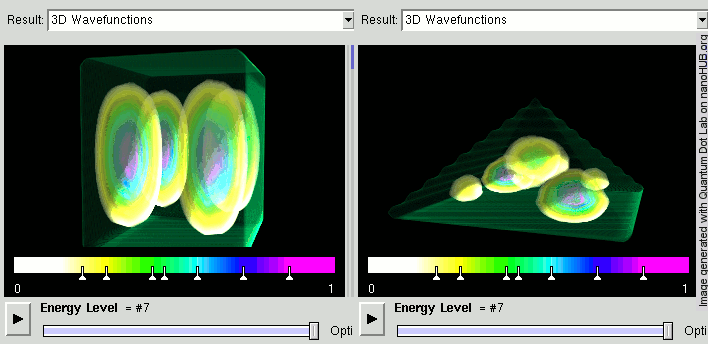
La densité de présence est indiquée par les couleurs.
Et avec une énergie potentielle ?
Par exemple, prenons l'atome d'hydrogène. Au centre, il y a un proton très lourd, donc quasi immobile. Il a une charge électrique qui génère un potentiel V(r) proportionnel à 1/r, où r est la distance au proton.
On peut calculer la fonction d'onde de l'électron de cette façon. C'est un calcul un peu lourd à faire, mais qui grosso modo a valu le prix Nobel à Schrödinger.
Les états d'énergie purs s'appellent les orbitales de l'atome, il y en a une liste quantifiée, assez compliquée mais pas trop non plus. On peut représenter la liste des orbitales, ça fait des trucs comme ça :
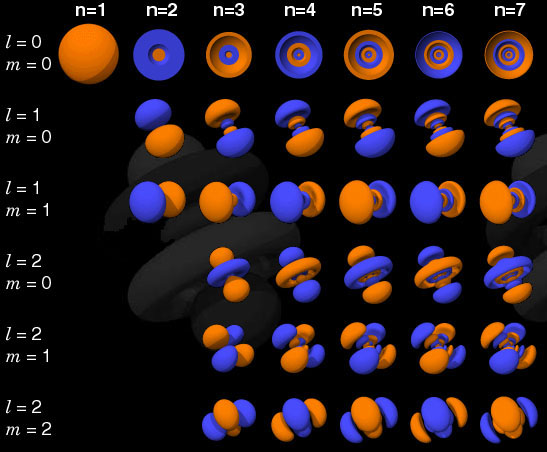
Un atome a une liste d'électrons, chacun d'entre eux est dans un état qui est l'une de ces orbitales, c'est ainsi que commence la chimie...
 Pavé
Pavé
 Quelques gif de quelques Mo
Quelques gif de quelques Mo

 . Qui serait une somme de sinusoïdes planes mais qui sont non seulement d'amplitudes différentes mais dans des plans différents... En fait ce qui se passe c'est que chacune de ces sinusoïdes tourne autour de l'axe sans changer de forme par ailleurs, c'est bien ça ? à une fréquence proportionnelle au carré de son nombre de ventres.)
. Qui serait une somme de sinusoïdes planes mais qui sont non seulement d'amplitudes différentes mais dans des plans différents... En fait ce qui se passe c'est que chacune de ces sinusoïdes tourne autour de l'axe sans changer de forme par ailleurs, c'est bien ça ? à une fréquence proportionnelle au carré de son nombre de ventres.). Qui serait une somme de sinusoïdes planes mais qui sont non seulement d'amplitudes différentes mais dans des plans différents... En fait ce qui se passe c'est que chacune de ces sinusoïdes tourne autour de l'axe sans changer de forme par ailleurs, c'est bien ça ? à une fréquence proportionnelle au carré de son nombre de ventres.)
)

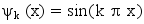 .
.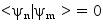 pour n et m deux entiers distincts, c'est un exercice de calcul intégral très classique. Ça signifie que les états ψk sont orthogonaux.
pour n et m deux entiers distincts, c'est un exercice de calcul intégral très classique. Ça signifie que les états ψk sont orthogonaux. => c'est la décomposition de Fourier.
=> c'est la décomposition de Fourier. , pour chaque point x de ]0,1[.
, pour chaque point x de ]0,1[. et
et  ont un produit scalaire nul si x et y sont différents. De plus toute fonction d'onde psi s'écrit comme somme de Diracs coefficientés (voir quand même plus bas).
ont un produit scalaire nul si x et y sont différents. De plus toute fonction d'onde psi s'écrit comme somme de Diracs coefficientés (voir quand même plus bas). correspond une mesure x de la position de la particule.
correspond une mesure x de la position de la particule. de L²([0,1]) correspondante, et à chaque vecteur de cette base est associé une mesure possible
de L²([0,1]) correspondante, et à chaque vecteur de cette base est associé une mesure possible  de cet observable.
de cet observable. est projetée sur l'un des états purs
est projetée sur l'un des états purs  , de façon non prédictible mais une probabilité proportionnelle à
, de façon non prédictible mais une probabilité proportionnelle à  . La quantité mesurée est le
. La quantité mesurée est le  correspondant au
correspondant au  sur lequel on est tombé.
sur lequel on est tombé. .
. .
. sont les Dirac
sont les Dirac  .
.



 est défini de façon tout à fait rigoureuse et satisfaisante.
est défini de façon tout à fait rigoureuse et satisfaisante.

 c'est génialissime ton analogie, je veux baffer tous les profs de MQ qui ont pas osé nous dire ça avant
c'est génialissime ton analogie, je veux baffer tous les profs de MQ qui ont pas osé nous dire ça avant 

est projetée sur l'un des états purs

 j'imagine qu'il faut des définitions mathématiques plus rigoureuses et c'est là qu'on a besoin des distributions c'est ça?
j'imagine qu'il faut des définitions mathématiques plus rigoureuses et c'est là qu'on a besoin des distributions c'est ça?est défini de façon tout à fait rigoureuse et satisfaisante.

 Ou alors je prends une pointe qui n'est que modérément pointue...
Ou alors je prends une pointe qui n'est que modérément pointue... ), la version "mathématicienne" est plus compliquée, il doit y avoir des conditions supplémentaires (mais là, sur le coup, je ne saurais l'énoncer...)
), la version "mathématicienne" est plus compliquée, il doit y avoir des conditions supplémentaires (mais là, sur le coup, je ne saurais l'énoncer...)
 où a et b sont deux nombres complexes.
où a et b sont deux nombres complexes.
 .
. , alors on peut dire que sans ambiguïté le premier qubit est dans l'état
, alors on peut dire que sans ambiguïté le premier qubit est dans l'état et le second est dans l'état
et le second est dans l'état .
. ne peut pas s'écrire sous cette forme.
ne peut pas s'écrire sous cette forme.