Aller de 1 à 0 est possible, ça veut dire que le produit est vide, et donc égal à 1 (l'élément neutre de la multiplication).
Nil Le 08/07/2007 à 12:41 Mais si on autorise à aller de 1 à 0, pourquoi n'autorise-t'on pas à descendre encore plus ? (comme j'ai dit plus haut, les maths c'est pas vraiment ma tasse de thé même si ça m'intéresse dans le principe).
Nil Le 08/07/2007 à 14:29 (pt1 c'est là où je me rends compte que j'ai totalement perdu le peu que j'avais en maths, c'est que bien que je comprenne tout à fait les conventions d'écritures employées, pour la somme et le produit, elles ne me parlent pas spontanément, je suis obligé de me forcer pour comprendre).
Tu veux qu'on en garde juste la moitié ?

<<< Kernel Extremis©®™ >>> et Inventeur de la différence administratif/judiciaire ! (©Yoshi Noir)
<Vertyos> un poil plus mais elle suce bien quand même la mienne ^^
<Sabrina`> tinkiete flan c juste qu'ils sont jaloux que je te trouve aussi appétissant
Nil Le 09/07/2007 à 02:52 Ben sauf que quand tu as un bonbon d'un côté puis que tu en as un d'un autre, quand tu les mets ensemble, ça fait quand même deux bonbons, donc il y a quand même un lien avec une certaine logique qui existe à la base, parce qu'à l'origine les mathématiques servaient à décrire des situations réelles (les prémices de l'économie/gestion, d'une certaine manière)
Mais même "deux" doit être défini (par exemple comme succ(succ(0)) ou |{{},{{}}}|).
voilà c'est tout à fait ça
Les droits inaliénables du troll :
1) le droit d'avoir raison
2) le droit d'être péremptoire
3) le droit de ne pas lire
4) le droit de ne pas répondre
5) le droit d'être de mauvaise foi
6) Autant pour moi / Faignant / Vivent Tintin et Milou





 ) mais est-ce que ca n'aurait vraiment "aucun sens" ou est-ce que ce serait juste pas pratique du tout ?
) mais est-ce que ca n'aurait vraiment "aucun sens" ou est-ce que ce serait juste pas pratique du tout ?  .
.


 ({}) = e
({}) = e
 )).
)).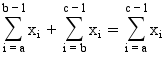

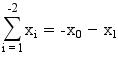
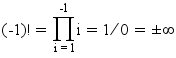


 )
) )
)